reading-notes

Trees

Reading

• Trees

Notes

Summary of Binary Tree Search Methods

• Pre-order: root >> left >> right
• In-order: left >> root >> right
• Post-order: left >> right >> root

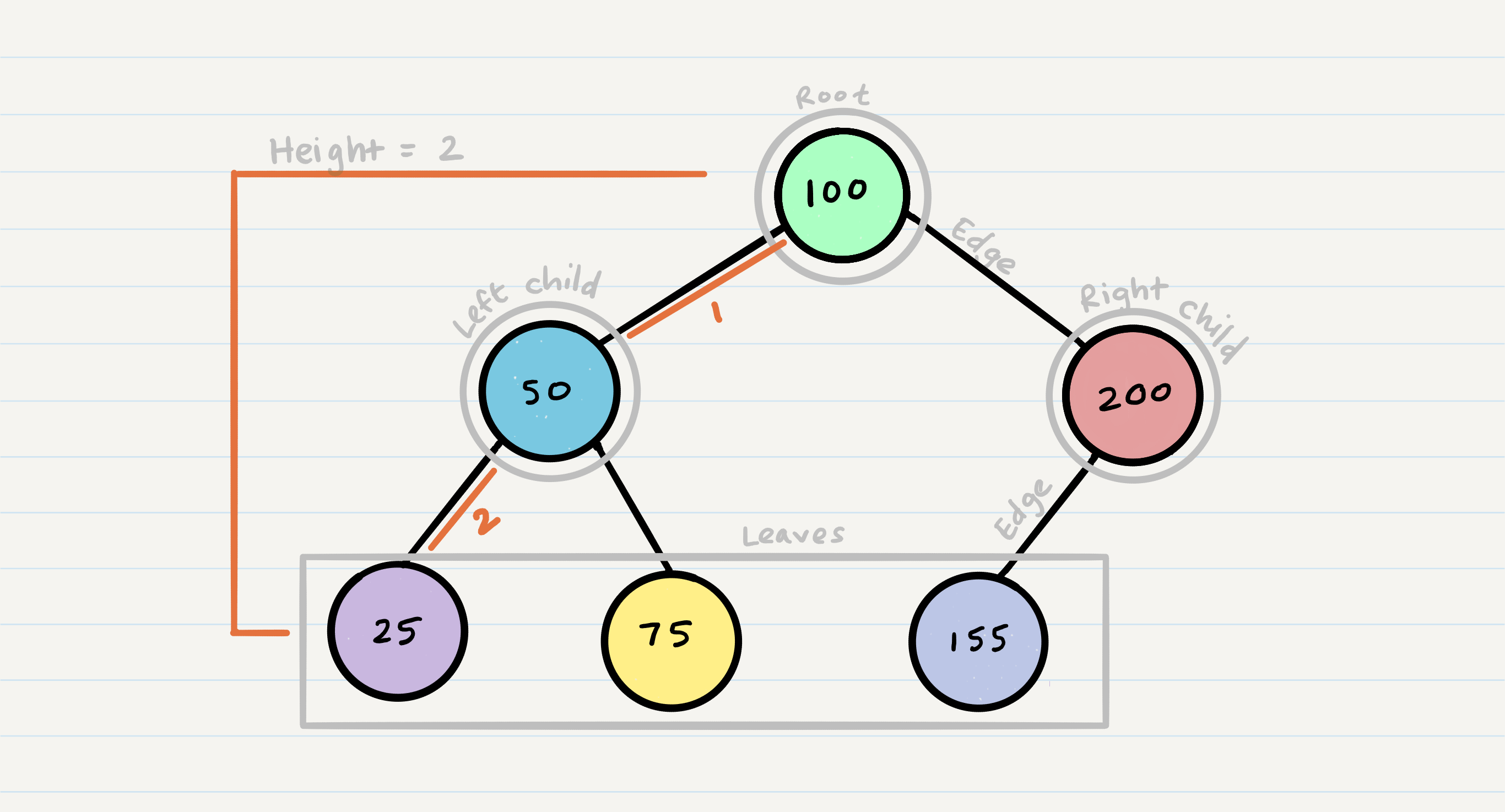
What is a tree?

A tree is a commonly used abstract data type that simulates a hierarchical tree structure, with a set of nodes or vertices, and edges connecting them. Each node in the tree has a value and may have one or more child nodes. The topmost node in the tree is called the root node, and there is no parent node for the root node. Each node in the tree, except for the root node, has exactly one parent node. The edges connecting the nodes represent the relationships between the nodes.

Trees are often used to represent hierarchical relationships between entities, such as the structure of a directory on a computer, or the relationships between elements in an XML document. They can also be used to represent decision-making structures, such as in a flowchart or a decision tree.

There are many different types of trees, including binary trees, AVL trees, red-black trees, and others, each with its own specific characteristics and applications.

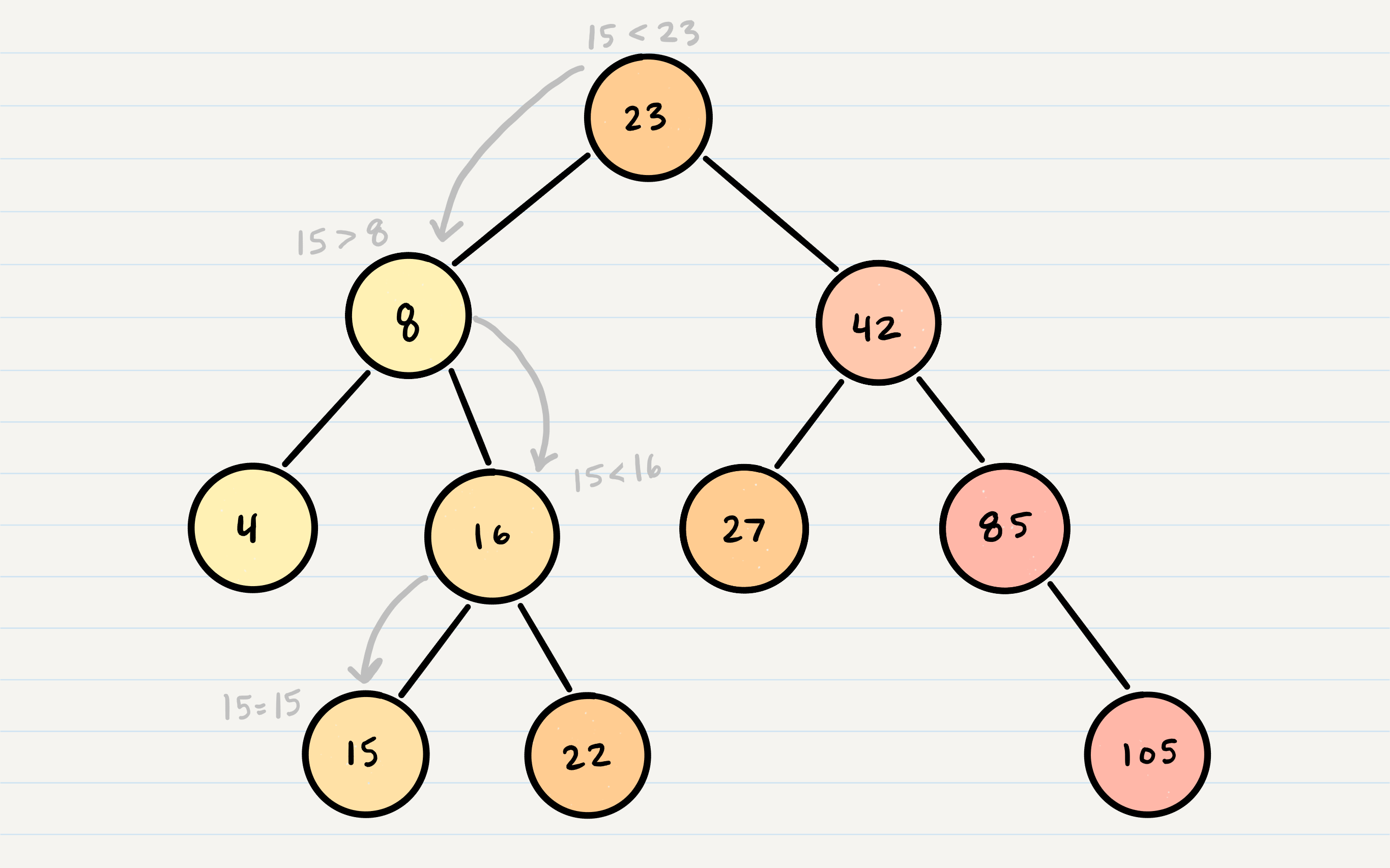
What is a binary search tree?

A binary search tree (BST) is a type of binary tree where the value of each node in the tree is greater than or equal to the values in its left child and less than or equal to the values in its right child. This property, known as the BST property, allows the tree to be searched quickly, making it a useful data structure for storing and accessing data.

The basic operations that can be performed on a binary search tree include inserting a new node, deleting a node, and searching for a particular node. The time complexity of these operations depends on the height of the tree, with the average-case time complexity being O(log n) for a tree with n nodes.

Binary search trees are used in a wide variety of applications, including computer science, engineering, and finance, where they can be used to store and quickly access data such as integers, floating point numbers, and strings.

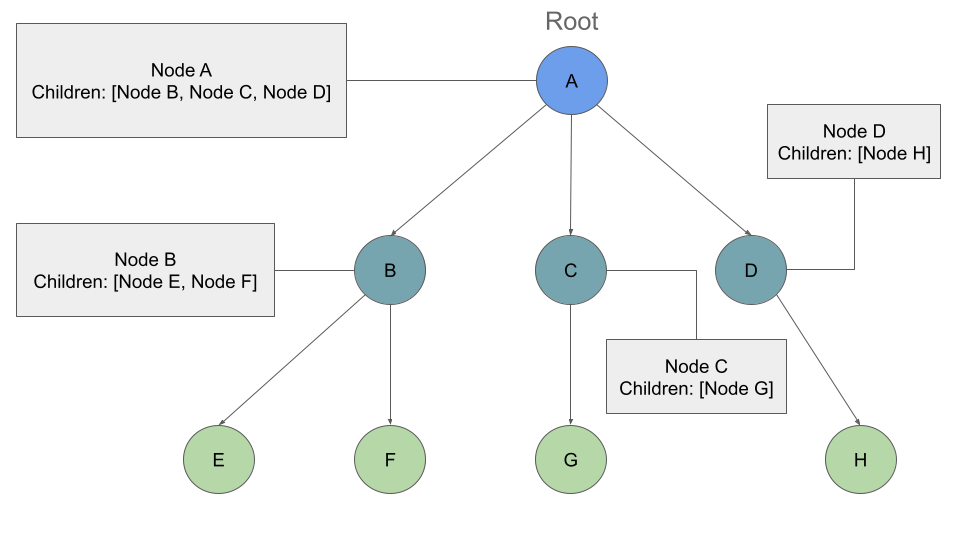
What is a K-Ary Tree?

A K-ary tree is a tree data structure in which each node can have up to K children. This is in contrast to a binary tree, which has a maximum of two children (known as left and right children), or a ternary tree, which has a maximum of three children.

K-ary trees are often used when it is necessary to store and access data that has a hierarchical structure, such as a file system or a database index. They can be searched and modified efficiently, with the time complexity of the basic operations (insertion, deletion, and search) being O(log n) on average for a tree with n nodes.

One of the main advantages of K-ary trees is that they can have a smaller height (i.e., the maximum distance from the root to a leaf node) than binary trees with the same number of nodes, which can make them more efficient in terms of space and time complexity. However, they do require more space to store the additional child pointers for each node.

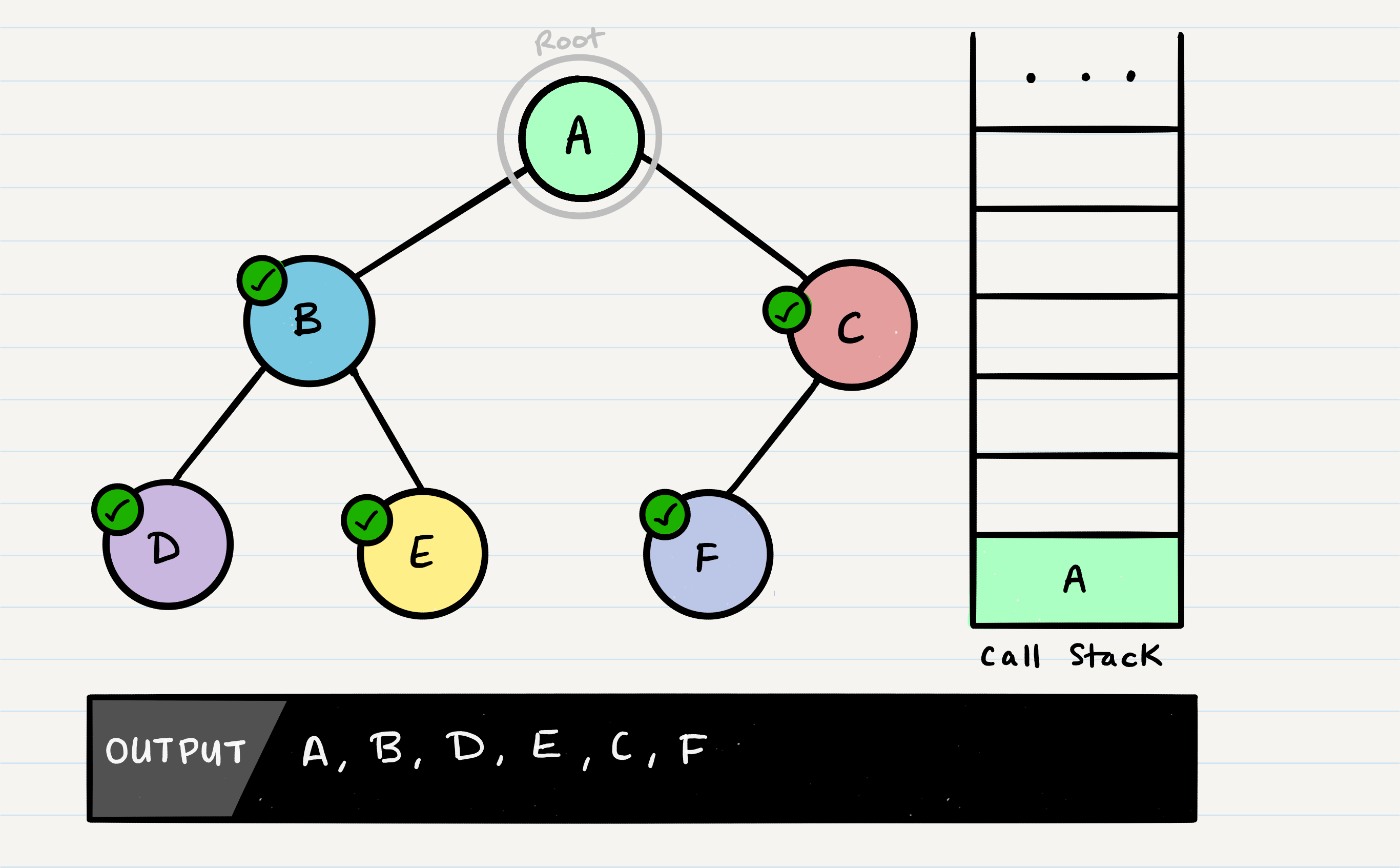
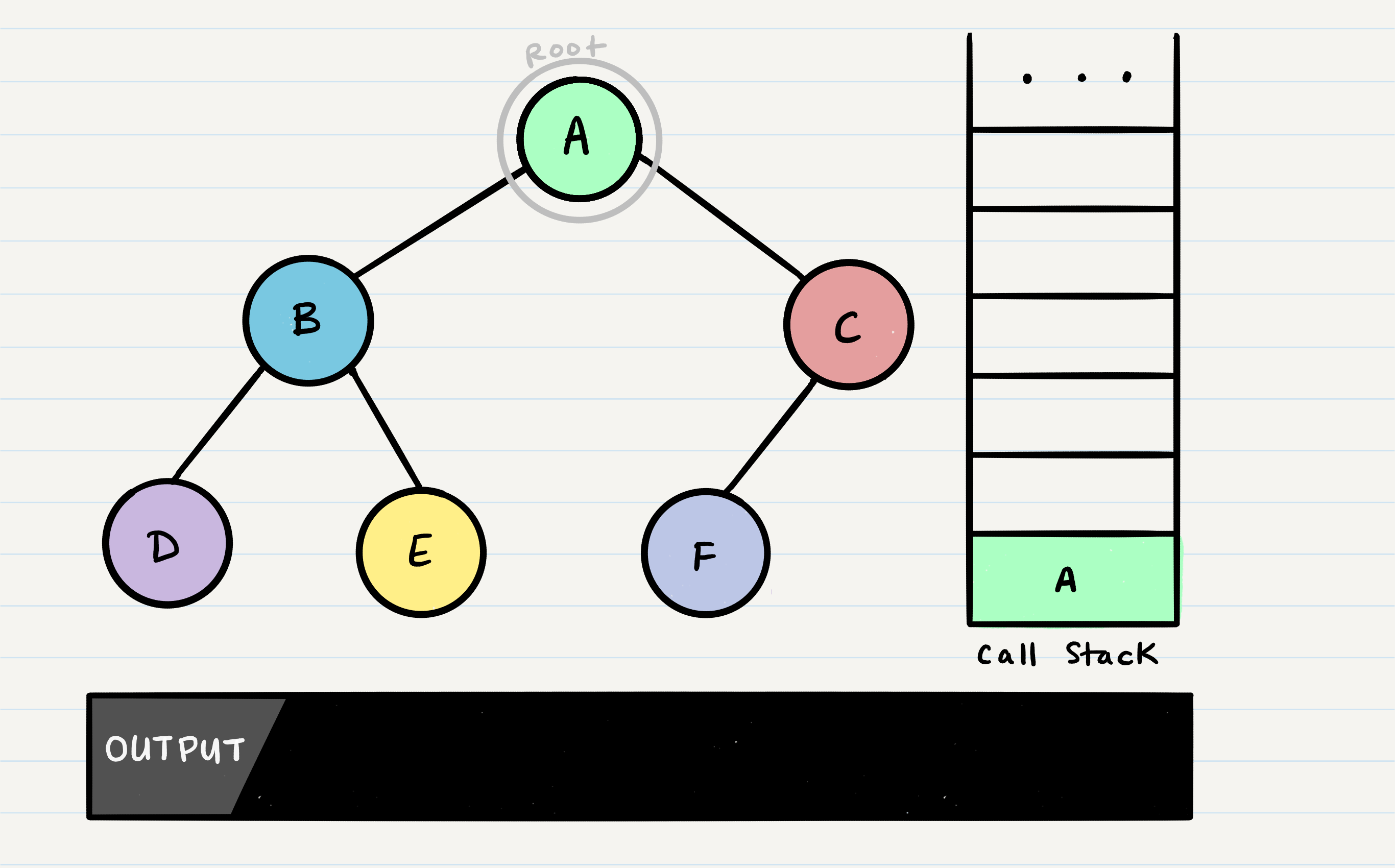
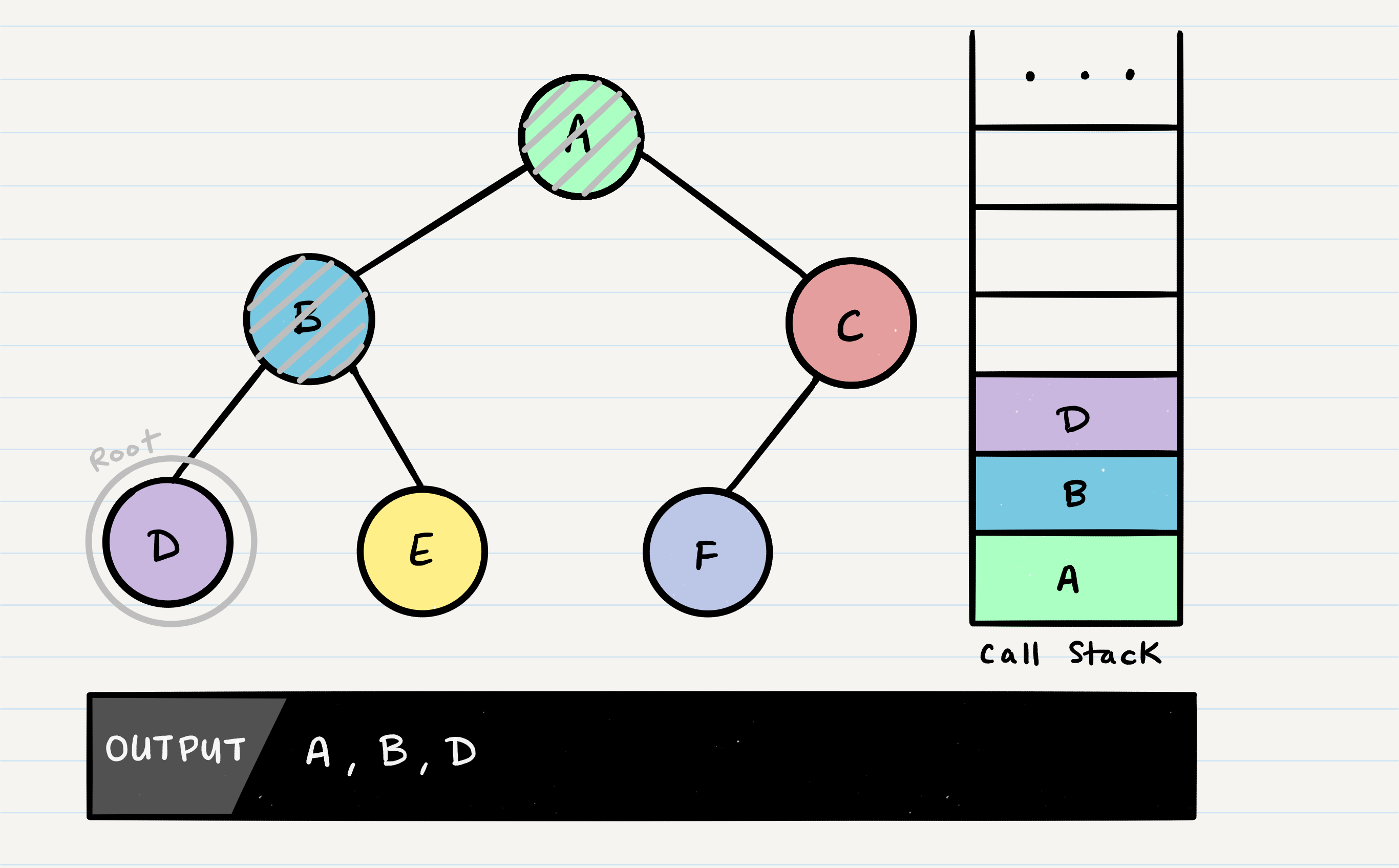
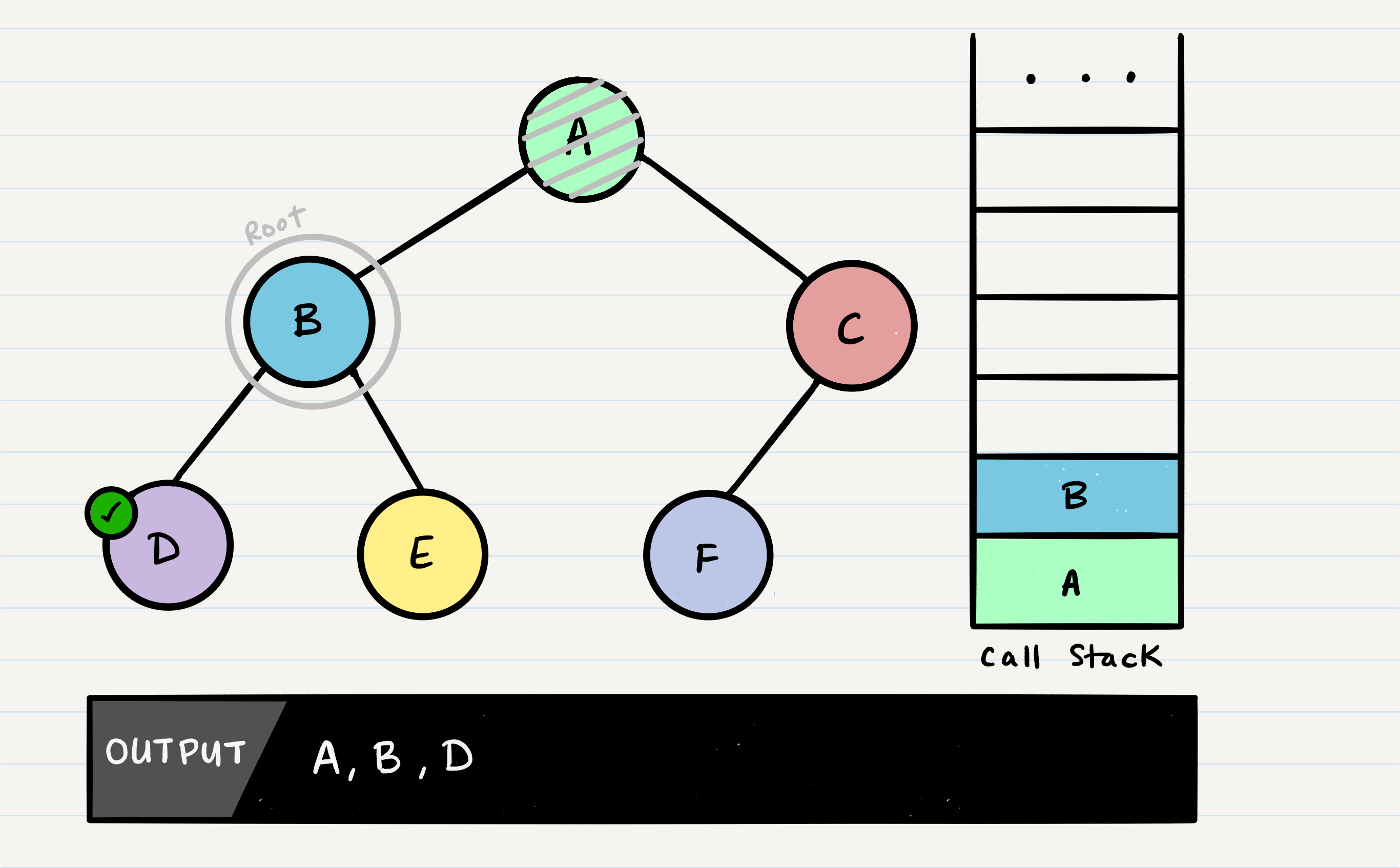
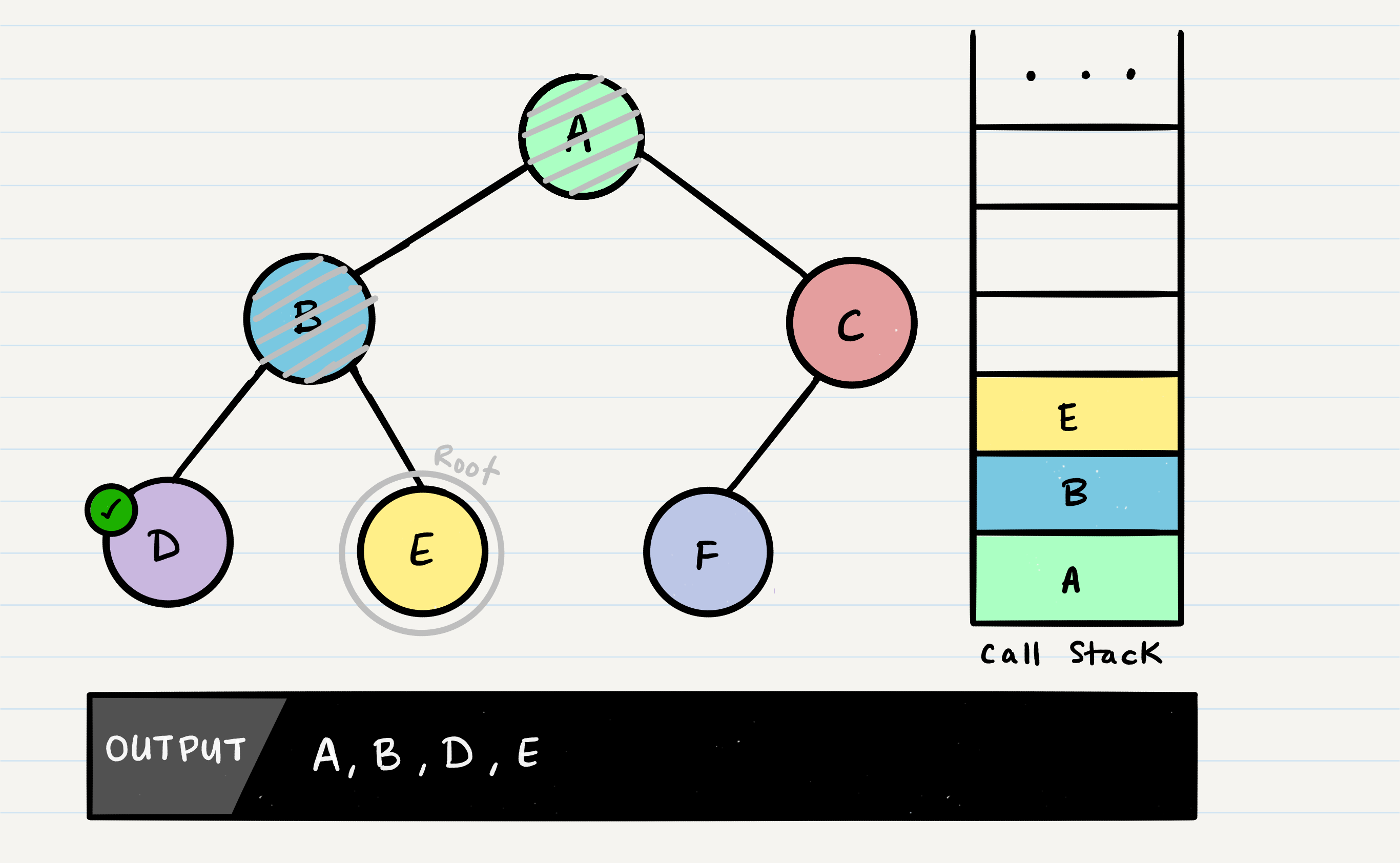
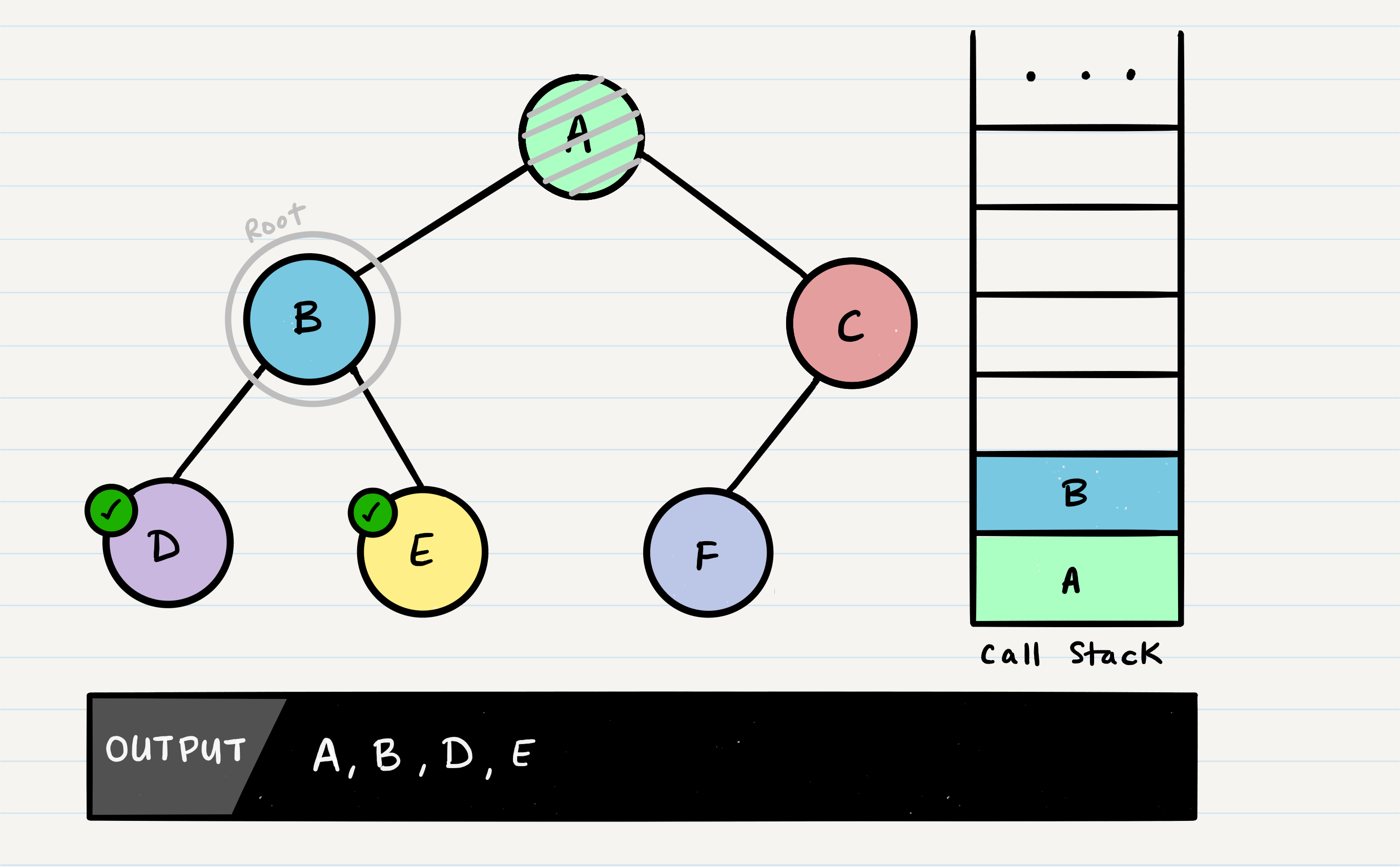
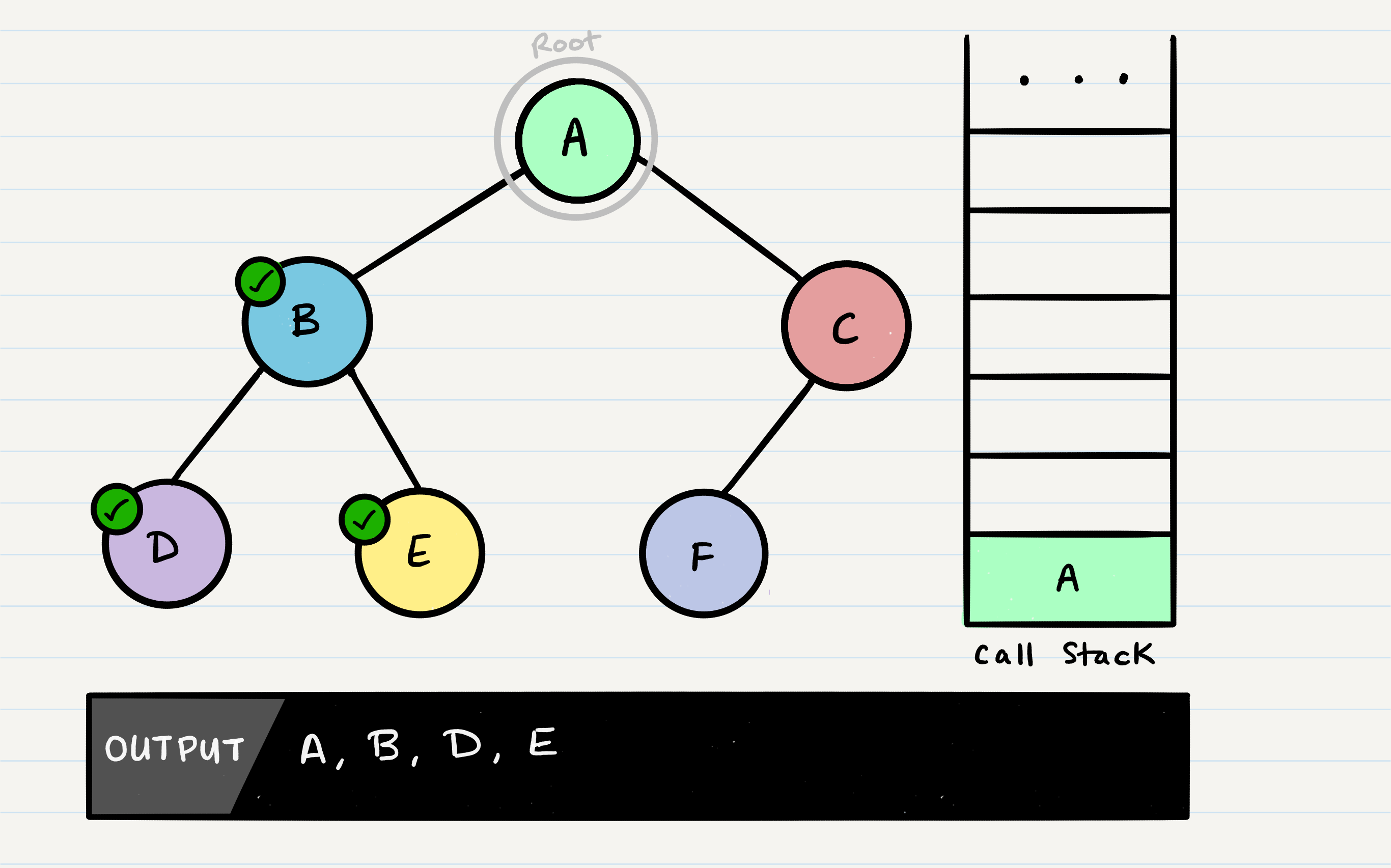
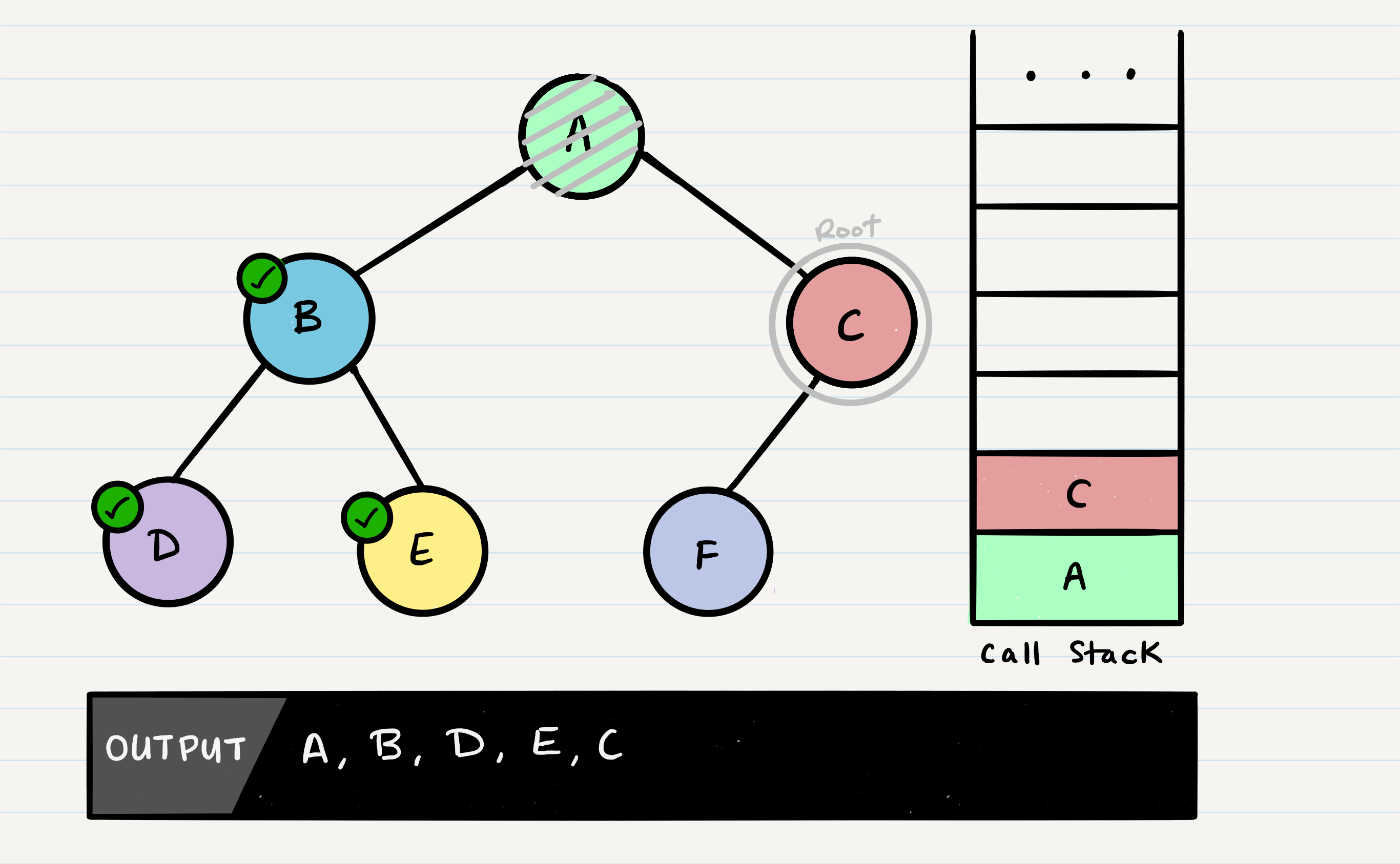
What is depth first traversal?

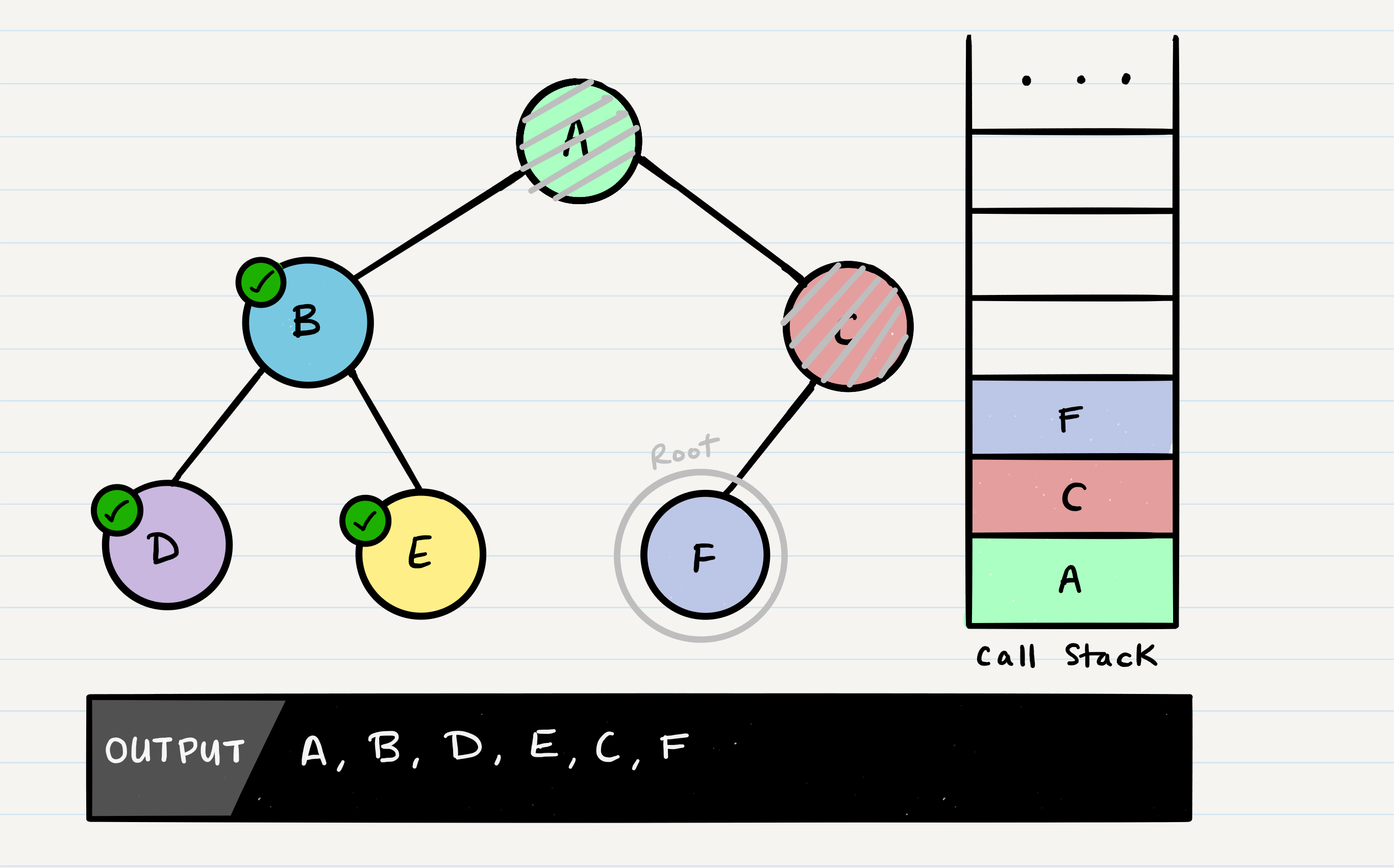
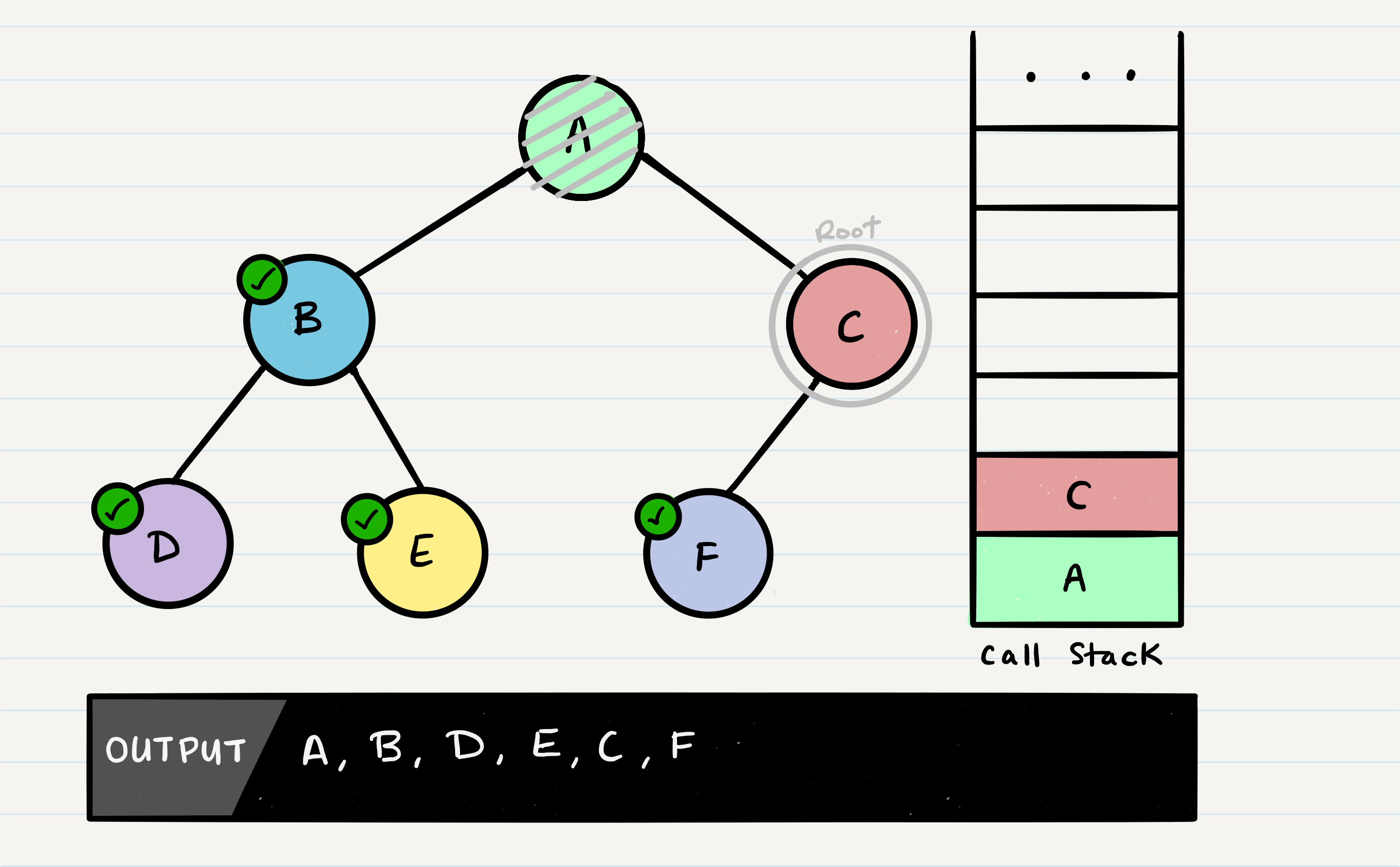
Depth first traversal is a method of traversing a tree or graph data structure in which the algorithm begins at the root node and explores as far as possible along each branch before backtracking. There are three common methods of depth first traversal: in-order, pre-order, and post-order.

In an in-order traversal, the left subtree of the current node is visited first, then the current node itself, and finally the right subtree. This results in the nodes being visited in ascending order, if the tree is a binary search tree.

In a pre-order traversal, the current node is visited first, followed by the left subtree, and then the right subtree.

In a post-order traversal, the left subtree is visited first, followed by the right subtree, and finally the current node itself.

Depth first traversal is often used to search for a specific node in a tree, or to visit all the nodes in the tree in a specific order. It can also be used to generate a topological sort of a directed acyclic graph (DAG).

class Node:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def pre_order_traverse(node):
    if node:
        print(node.value)
        pre_order_traverse(node.left)
        pre_order_traverse(node.right)

root = Node(1, Node(2, Node(4), Node(5)), Node(3, Node(6), Node(7)))
pre_order_traverse(root)

This will print the values of the nodes in the following order: 1, 2, 4, 5, 3, 6, 7.

To implement an in-order or post-order traversal, you would simply need to adjust the order in which the left, current, and right nodes are visited.

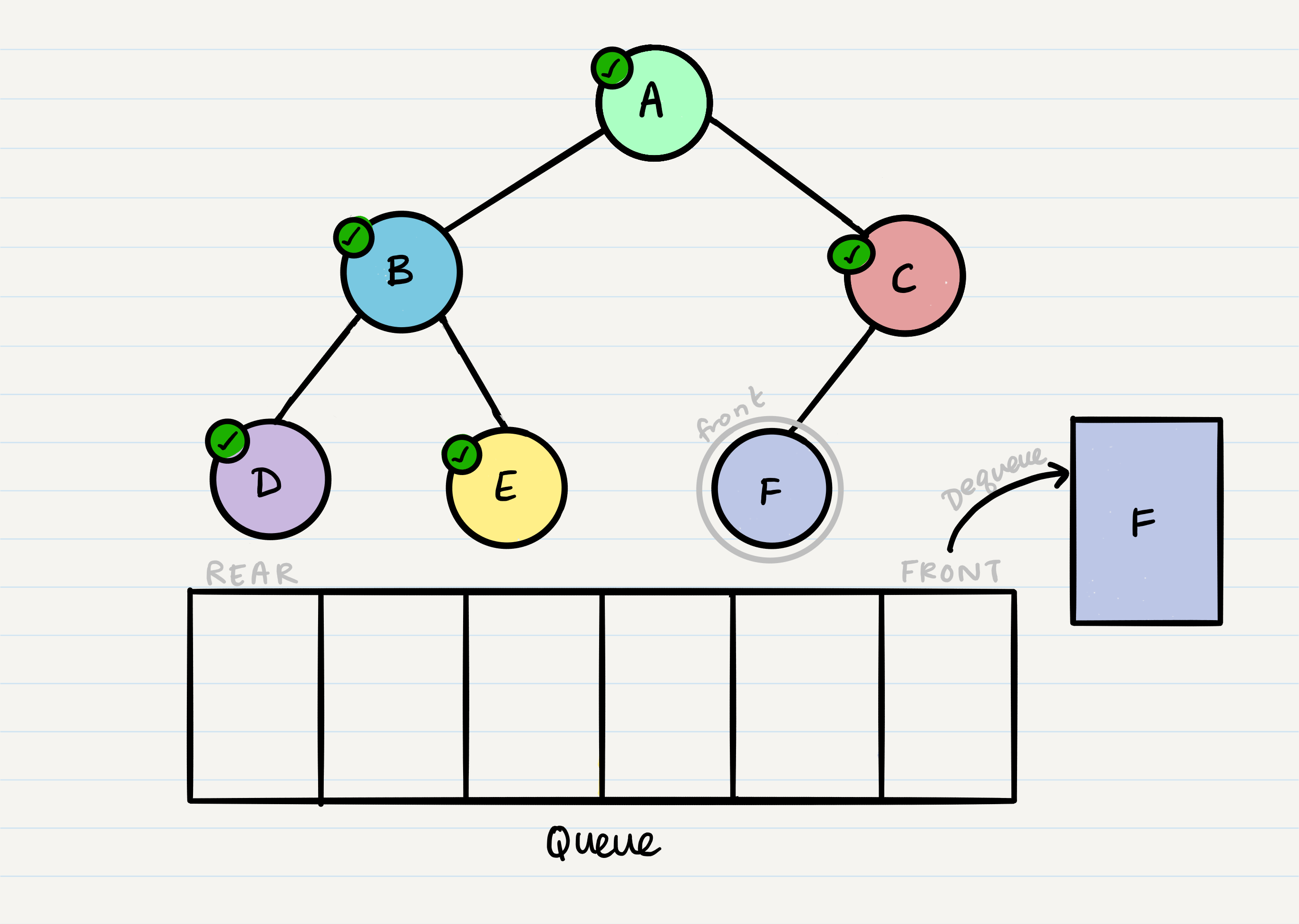
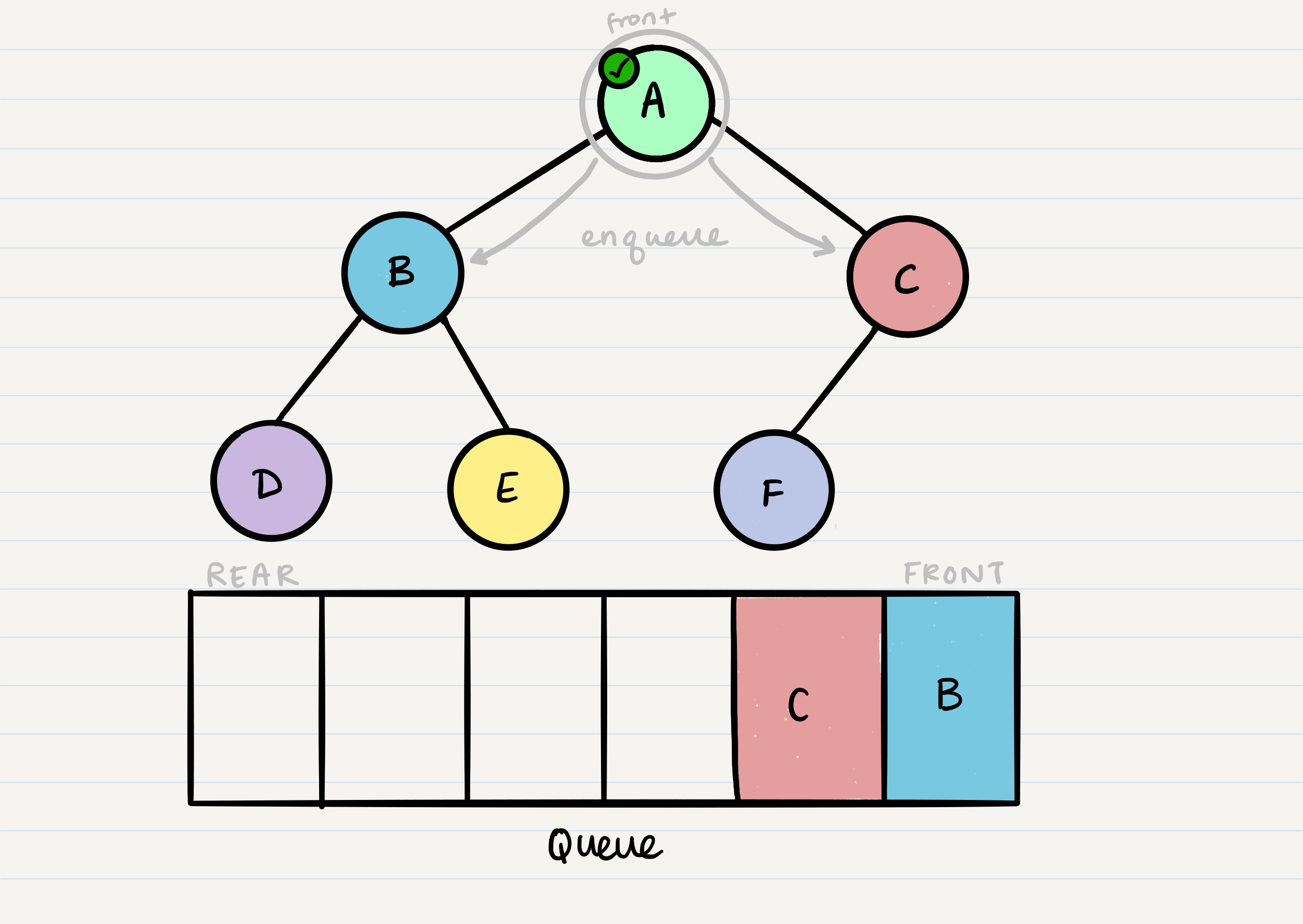
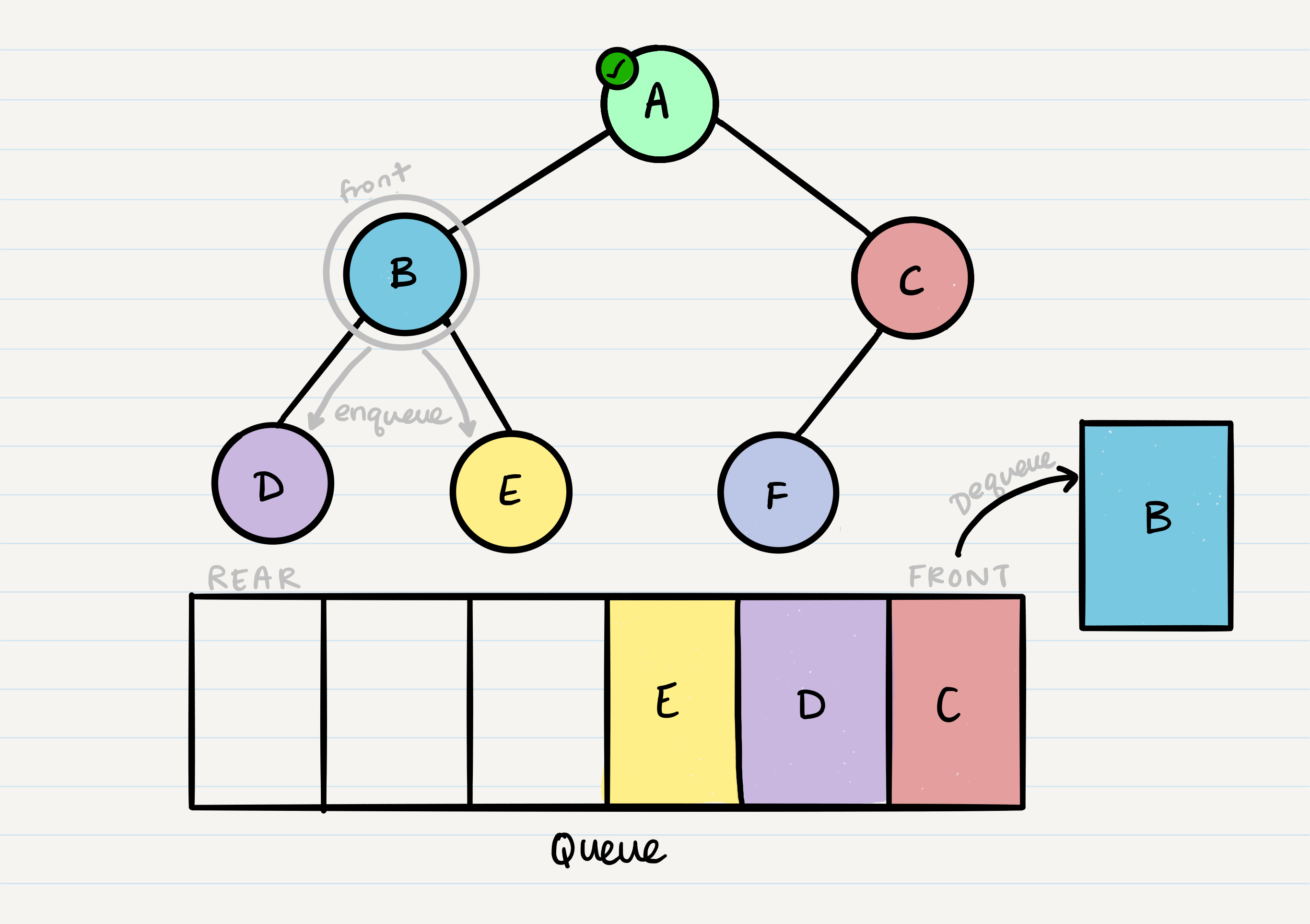
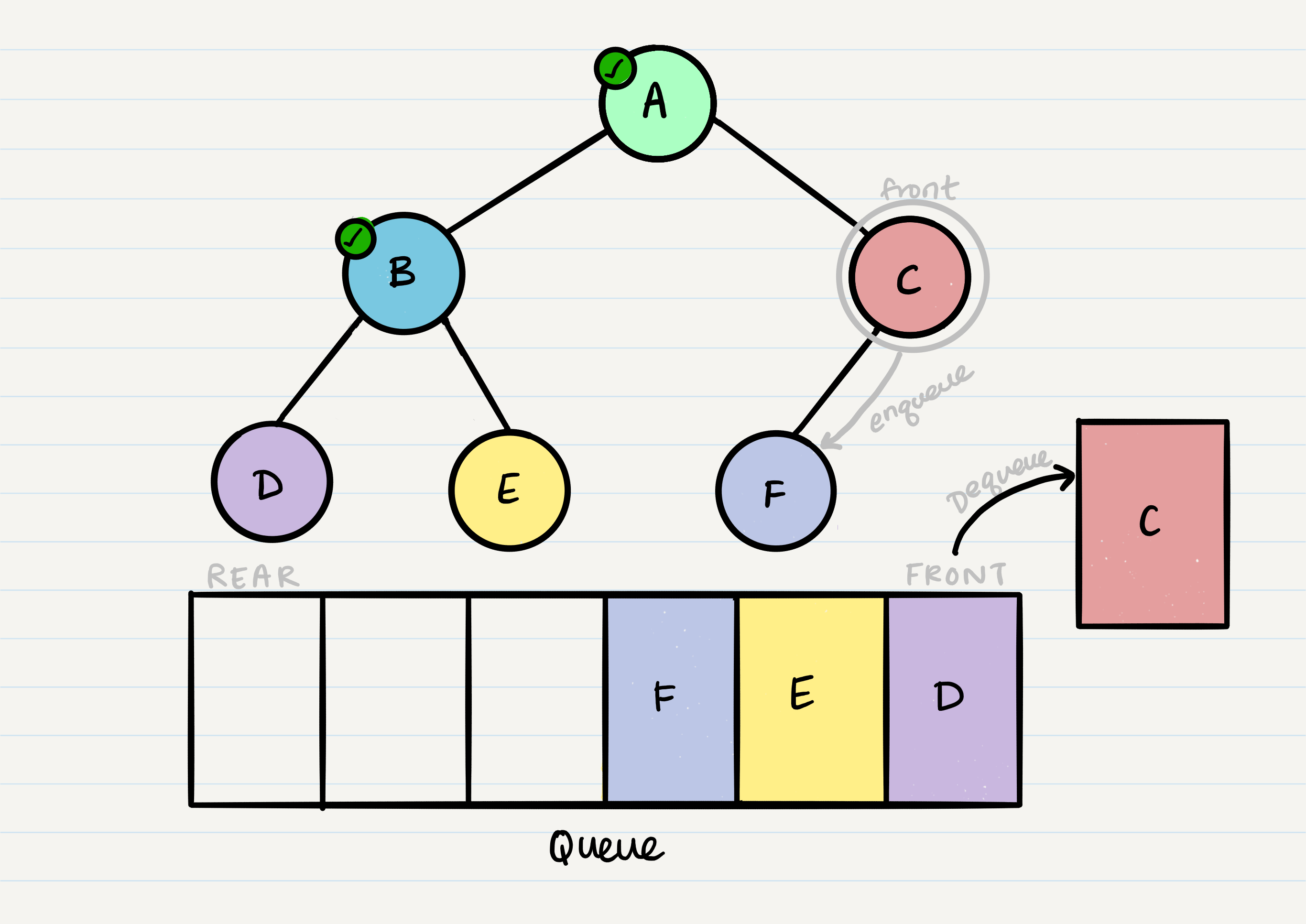
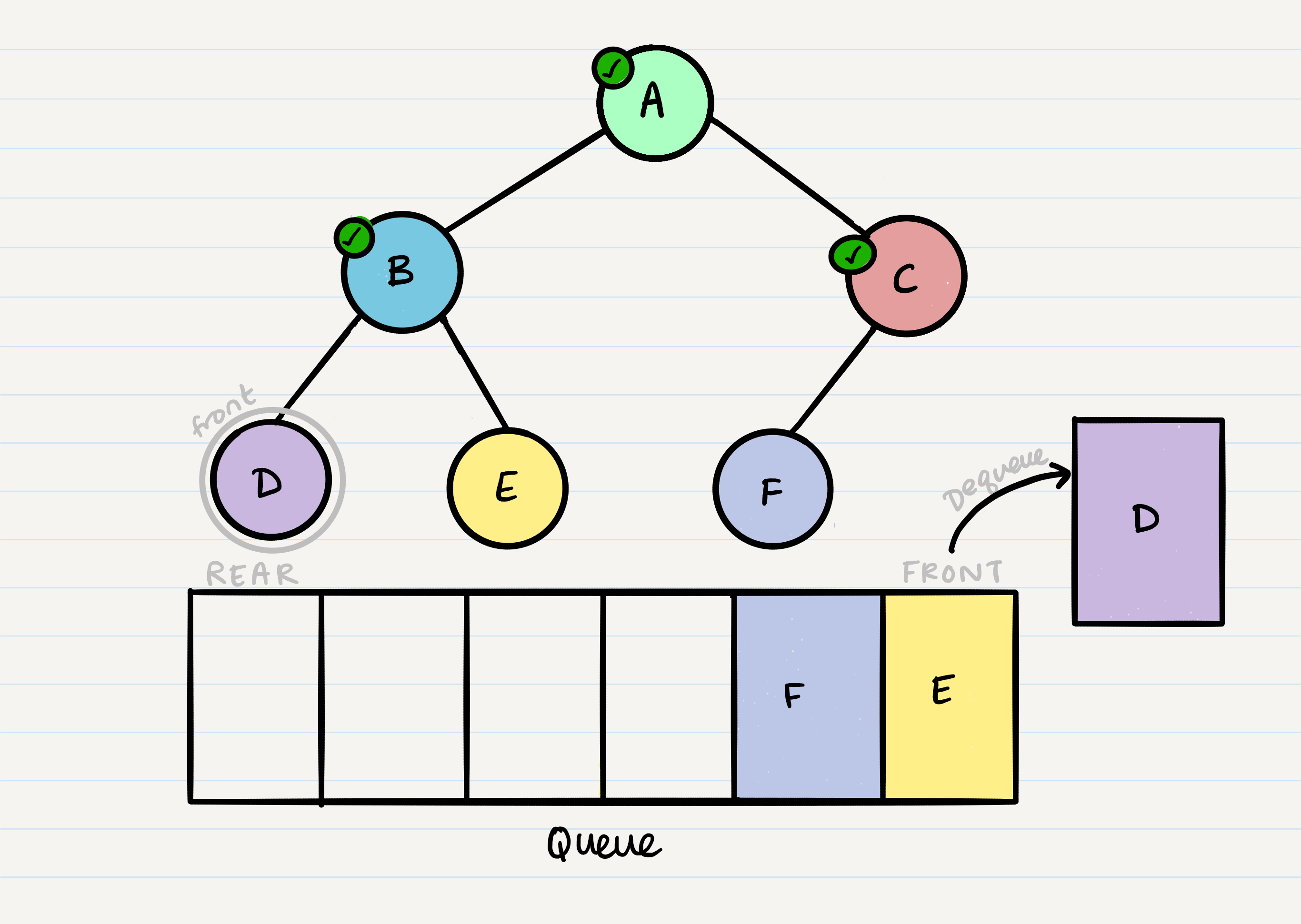
What is breadth first traversal?

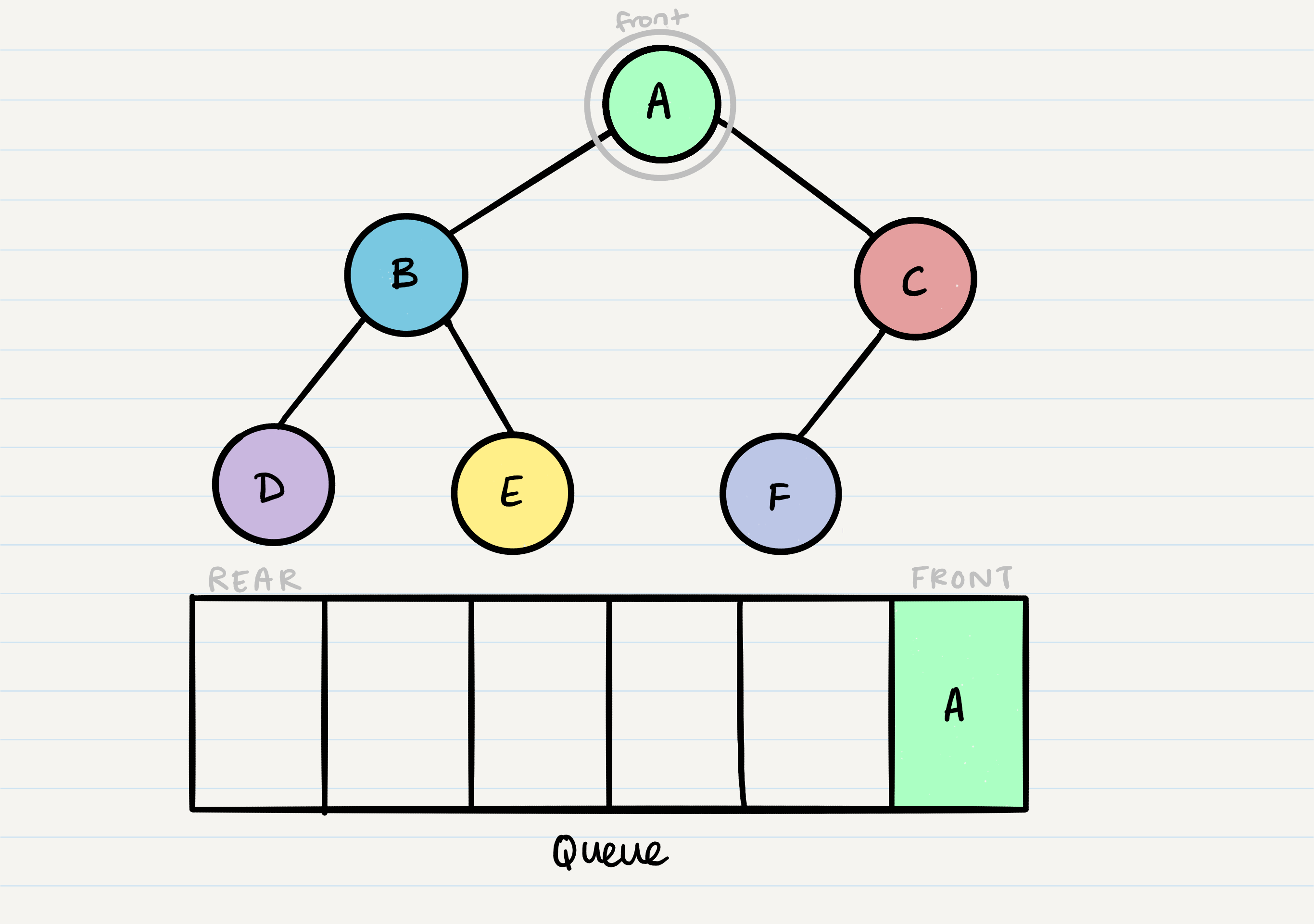
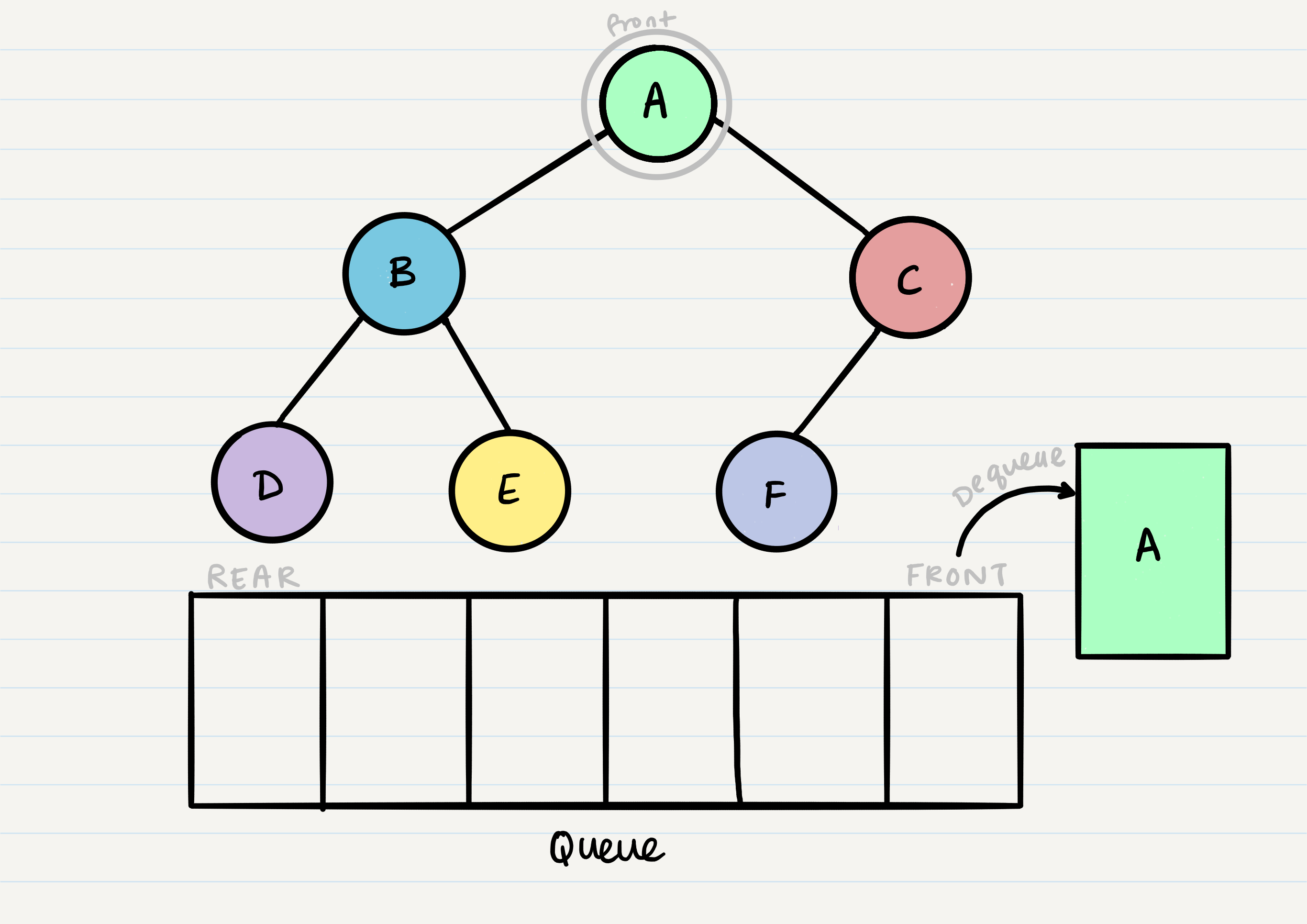
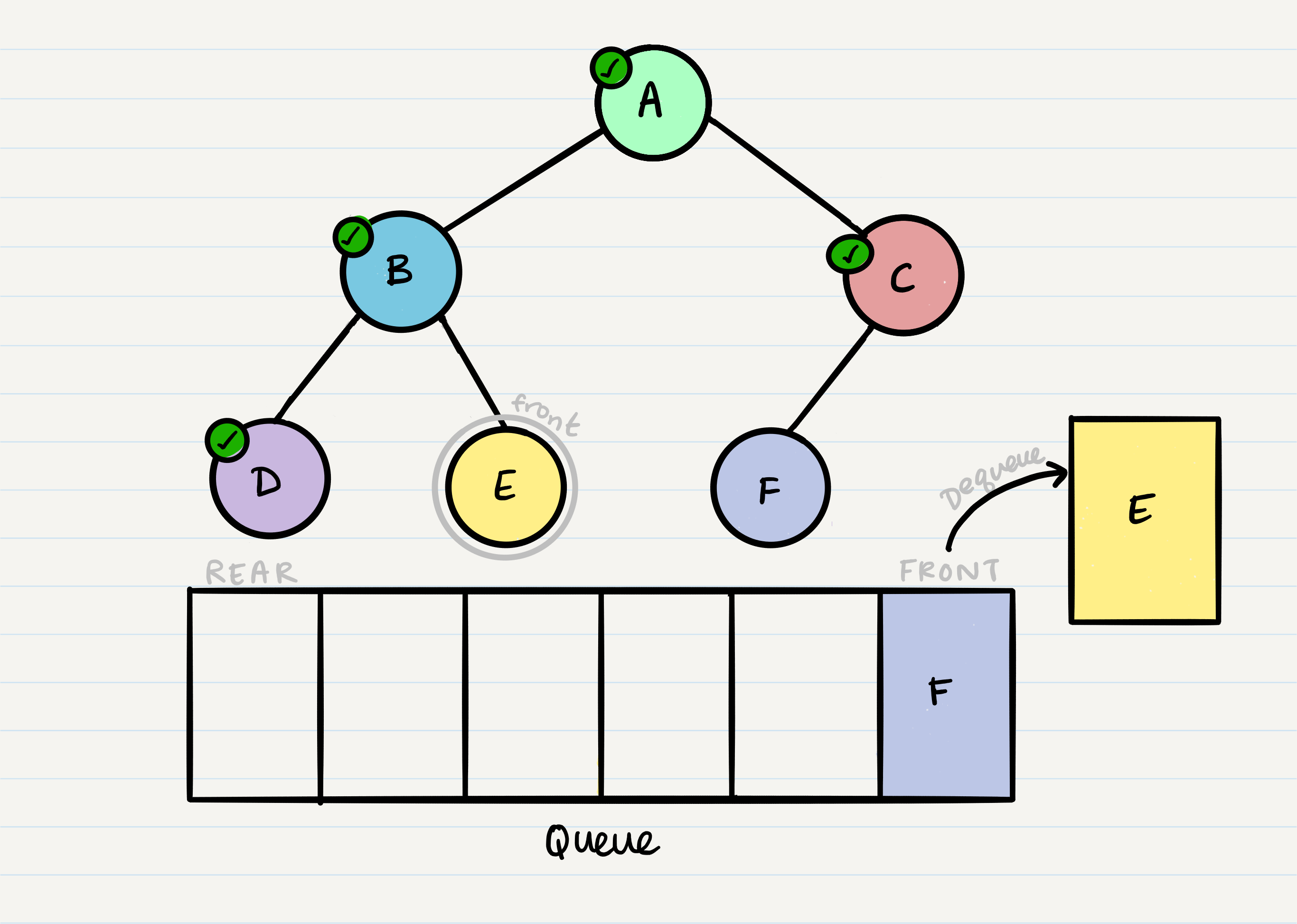
Breadth first traversal is a method of traversing a tree or graph data structure in which the algorithm begins at the root node and explores all the neighboring nodes at the present depth level before moving on to the nodes at the next depth level.

In a breadth first traversal, the nodes are visited in the order in which they are encountered, starting at the root node and moving across each level of the tree from left to right. This can be implemented using a queue to store the nodes that are waiting to be visited.

Breadth first traversal is often used to search for a specific node in a tree, or to visit all the nodes in the tree in a specific order. It can also be used to find the shortest path between two nodes in a graph, or to solve other problems such as finding the shortest path in a maze.

class Node:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def breadth_first_traverse(root):
    queue = [root]
    while queue:
        node = queue.pop(0)
        print(node.value)
        if node.left:
            queue.append(node.left)
        if node.right:
            queue.append(node.right)

root = Node(1, Node(2, Node(4), Node(5)), Node(3, Node(6), Node(7)))
breadth_first_traverse(root)

This will print the values of the nodes in the following order: 1, 2, 3, 4, 5, 6, 7.

Code for Binary Tree and Binary Search Tree

class BinaryTree:

    def __init__(self, root=None):
        self.root = root

    def pre_order(self):
        values = []
        stack = [self.root]
        while stack:
            node = stack.pop()
            values.append(node.value)
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return values

    def in_order(self):
        values = []
        stack = []
        node = self.root
        while stack or node:
            while node:
                stack.append(node)
                node = node.left
            node = stack.pop()
            values.append(node.value)
            node = node.right
        return values

    def breadth_first(self):
        values = []
        queue = [self.root]
        while queue:
            node = queue.pop(0)
            values.append(node.value)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        return values


    def post_order(self):
        values = []
        stack = [self.root]
        while stack:
            node = stack.pop()
            values.append(node.value)
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)
        return values[::-1]

class Node:
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

Binary Tree Methods

• pre_order(): This method performs a pre-order traversal of the binary tree and returns a list of the values of the nodes in the tree. It uses a stack to store the nodes that are waiting to be visited. It first adds the current node to the list of values, then pushes the right and left child nodes onto the stack if they exist. The time complexity of this method is O(n), where n is the number of nodes in the tree. This is because each node in the tree is visited exactly once.
• in_order(): This method performs an in-order traversal of the binary tree and returns a list of the values of the nodes in the tree. It uses a stack to store the nodes that are waiting to be visited. It first pushes the current node and all of its left child nodes onto the stack, then adds the value of the current node to the list of values and sets the current node to its right child. If the current node has no right child, it pops the top node from the stack and repeats the process. The time complexity of this method is also O(n). This is because each node in the tree is visited exactly once.
• post_order(): This method performs a post-order traversal of the binary tree and returns a list of the values of the nodes in the tree. It uses a stack to store the nodes that are waiting to be visited. It first pushes the current node and all of its child nodes onto the stack, then adds the value of the current node to the list of values and sets the current node to the top node of the stack. If the current node has no children, it pops the top node from the stack and repeats the process. The final list of values is reversed to achieve the correct order. The time complexity of this method is also O(n). This is because each node in the tree is visited exactly once.

from data_structures.binary_tree import BinaryTree, Node

class BinarySearchTree(BinaryTree):
   
   def add(self, value):
        new_node = Node(value)
        if not self.root:
            self.root = new_node
            return

        node = self.root
        while True:
            if value < node.value:
                if not node.left:
                    node.left = new_node
                    return
                node = node.left
            else:
                if not node.right:
                    node.right = new_node
                    return
                node = node.right

    def contains(self, value):
        node = self.root
        while node:
            if value == node.value:
                return True
            elif value < node.value:
                node = node.left
            else:
                node = node.right
        return False